Java将二进制树转换为二进制搜索树
在此程序中,我们需要将给定的二进制树转换为相应的二进制搜索树。如果每个节点最多有两个子代,则将一棵树称为二叉树。二进制搜索树是二进制树的一种特殊情况,其中根节点左侧的所有节点都应小于根节点,而右侧节点则应大于根节点。
通过将给定的二叉树转换为其相应的数组表示形式,可以解决此问题。对数组进行排序。从数组元素计算中间节点,因为它将成为相应的二进制搜索树的根节点。
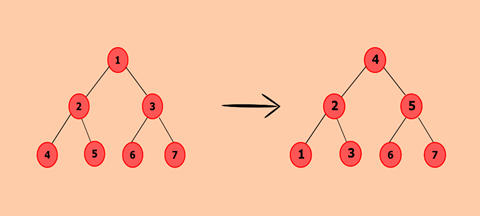
算法
定义Node类,它具有三个属性,即: 左和右数据。在这里,左代表节点的左子节点,右代表节点的右子节点。
创建节点后,数据将传递到该节点的data属性,并且左右都将设置为null。
定义另一个具有两个属性root和treeArray的类。 Root表示树的根节点,并将其初始化为null。 treeArray将存储二叉树的数组表示形式。
a.convertBTBST()会将二进制树转换为相应的二进制搜索树:
它将通过调用convertBTtoArray()将二叉树转换为相应的数组。
从步骤1开始按升序排列结果数组。
通过调用createBST()将数组转换为二进制搜索树。
calculateSize()将计算树中存在的节点数。
convertBTtoArray()将遍历二叉树并将其添加到treeArray中,从而将二叉树转换为其数组表示形式。
createBST()将通过选择已排序的treeArray的中间节点作为其根节点来创建相应的二进制搜索树。 treeArray将分为两部分,即[0,mid-1]和[mid + 1,end]。从每个数组中递归地找到中间节点,分别创建左子树和右子树。
Inorder()将按顺序显示树的节点,即左子节点,后跟根节点,右子节点。
程序:
import java.util.Arrays;
public class ConvertBTtoBST {
//Represent a node of binary tree
public static class Node{
int data;
Node left;
Node right;
public Node(int data){
//Assign data to the new node, set left and right children to null
this.data = data;
this.left = null;
this.right = null;
}
}
//Represent the root of binary tree
public Node root;
int[] treeArray;
int index = 0;
public ConvertBTtoBST(){
root = null;
}
//convertBTBST() will convert a binary tree to binary search tree
public Node convertBTBST(Node node) {
//Variable treeSize will hold size of tree
int treeSize = calculateSize(node);
treeArray = new int[treeSize];
//Converts binary tree to array
convertBTtoArray(node);
//Sort treeArray
Arrays.sort(treeArray);
//Converts array to binary search tree
Node d = createBST(0, treeArray.length -1);
return d;
}
//calculateSize() will calculate size of tree
public int calculateSize(Node node)
{
int size = 0;
if (node == null)
return 0;
else {
size = calculateSize (node.left) + calculateSize (node.right) + 1;
return size;
}
}
//convertBTtoArray() will convert the given binary tree to its corresponding array representation
public void convertBTtoArray(Node node) {
//Check whether tree is empty
if(root == null){
System.out.println("Tree is empty");
return;
}
else {
if(node.left != null)
convertBTtoArray(node.left);
//Adds nodes of binary tree to treeArray
treeArray[index] = node.data;
index++;
if(node.right != null)
convertBTtoArray(node.right);
}
}
//createBST() will convert array to binary search tree
public Node createBST(int start, int end) {
//It will avoid overflow
if (start > end) {
return null;
}
//Variable will store middle element of array and make it root of binary search tree
int mid = (start + end) / 2;
Node node = new Node(treeArray[mid]);
//Construct left subtree
node.left = createBST(start, mid - 1);
//Construct right subtree
node.right = createBST(mid + 1, end);
return node;
}
//inorder() will perform inorder traversal on binary search tree
public void inorderTraversal(Node node) {
//Check whether tree is empty
if(root == null){
System.out.println("Tree is empty");
return;
}
else {
if(node.left!= null)
inorderTraversal(node.left);
System.out.print(node.data + " ");
if(node.right!= null)
inorderTraversal(node.right);
}
}
public static void main(String[] args) {
ConvertBTtoBST bt = new ConvertBTtoBST();
//Add nodes to the binary tree
bt.root = new Node(1);
bt.root.left = new Node(2);
bt.root.right = new Node(3);
bt.root.left.left = new Node(4);
bt.root.left.right = new Node(5);
bt.root.right.left = new Node(6);
bt.root.right.right = new Node(7);
//Display given binary tree
System.out.println("Inorder representation of binary tree: ");
bt.inorderTraversal(bt.root);
//Converts binary tree to corresponding binary search tree
Node bst = bt.convertBTBST(bt.root);
//Display corresponding binary search tree
System.out.println("\nInorder representation of resulting binary search tree: ");
bt.inorderTraversal(bst);
}
}
输出:
Inorder representation of binary tree:
4 2 5 1 6 3 7
Inorder representation of resulting binary search tree:
1 2 3 4 5 6 7

