Java确定给定矩阵是否为稀疏矩阵
在此程序中,我们需要检查给定矩阵是否为稀疏矩阵。
如果矩阵的大多数元素为0,则称该矩阵为稀疏矩阵。这表示该矩阵包含的非零元素非常少。
检查给定矩阵是稀疏矩阵还是稀疏矩阵?不,我们首先计算矩阵中存在的零元素的数量。然后计算矩阵的大小。为了使矩阵稀疏,数组中存在的零个元素的数量必须大于size/2。
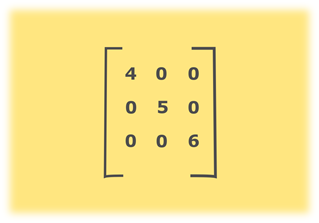
上述矩阵中存在的零数目为6,矩阵大小为3 * 3 =9。因为6> 4.5表示给定数组的大多数元素为零。因此,上述矩阵是一个稀疏矩阵。
算法
步骤1: START
步骤2: 定义rows,cols,size
步骤3: SET count= 0
步骤4: 初始化第一个矩阵 a[][] = {{4,0,0},{0,5,0},{0,0,6}}
步骤5: rows = a.length
步骤6: cols = a[0].length
步骤7: size = rows*cols
步骤8: 直到 i < rows
为止,将步骤9重复到步骤10 //for(i = 0; i < rows; i++)
步骤9: 重复步骤10,直到 j < cols
////for(j = 0; j < cols; j++)
步骤10: if(a[i][j] == 0) 然后count++
步骤11: if(count > size/2),然后打印"Yes",否则打印"No"
步骤12: END
程序
public class SparseMatrix
{
public static void main(String[] args) {
int rows, cols, size, count = 0;
//Initialize matrix a
int a[][] = {
{4, 0, 0},
{0, 5, 0},
{0, 0, 6}
};
//Calculates number of rows and columns present in given matrix
rows = a.length;
cols = a[0].length;
//Calculates the size of array
size = rows * cols;
//Count all zero element present in matrix
for(int i = 0;i <rows;i++){
for(int j = 0;j <cols;j++){
if(a[i][j] == 0)
count++;
}
}
if(count >(size/2))
System.out.println("Given matrix is a sparse matrix");
else
System.out.println("Given matrix is not a sparse matrix");
}
}
输出:
Given matrix is a sparse matrix



