Java显示下三角矩阵
在此程序中,我们需要显示下部三角形矩阵。
下部三角形矩阵
下三角矩阵是一个正方形矩阵,其中对角线上方的所有元素都为零。为了找到下三角矩阵,矩阵必须是正方形矩阵,也就是说,矩阵中的行数和列数必须相等。典型的正方形矩阵的尺寸可以用nx n表示。
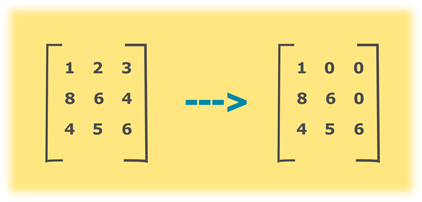
考虑以上示例,给定矩阵的主要对角元素为(1、6、6)。对角线上方的所有元素都必须设为零。在我们的示例中,这些元素位于位置(1、2),(1、3)和(2、3)。要将给定的矩阵转换为较低的三角矩阵,请遍历该矩阵并将列号大于行号的元素的值设置为零。
算法
步骤1: START
步骤2: 定义行,列
步骤3: 初始化矩阵a[][] = {{1,2,3},{8,6,4},{4,5,6}}
步骤4: rows= a.length
步骤5: cols = a [0] .length
步骤6: if(rows!= cols)
然后
PRINT"矩阵应为方阵"
else
转到步骤7
步骤7: 直到i < rows
为止,将步骤4重复到步骤6//for(i = 0; i < rows; i ++)
步骤8: 重复步骤9,直到j < cols //for(j=0; j < cols; j ++)
如果if(j> i),则PRINT 0 else PRINT a[i][j]
步骤9: 打印新行
第10步: END
程序
public class LowerTriangular
{
public static void main(String[] args) {
int rows, cols;
//Initialize matrix a
int a[][] = {
{1, 2, 3},
{8, 6, 4},
{4, 5, 6}
};
//Calculates number of rows and columns present in given matrix
rows = a.length;
cols = a[0].length;
if(rows != cols){
System.out.println("Matrix should be a square matrix");
}
else {
//Performs required operation to convert given matrix into lower triangular matrix
System.out.println("Lower triangular matrix: ");
for(int i = 0;i <rows;i++){
for(int j = 0;j <cols;j++){
if(j >i)
System.out.print("0 ");
else
System.out.print(a[i][j] + " ");
}
System.out.println();
}
}
}
}
输出:
Lower triangular matrix:
1 0 0
8 6 0
4 5 6



