Java查找具有N个键的可能的二进制搜索树的总数
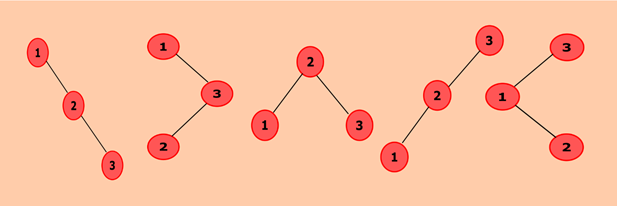
在此程序中,我们需要找出可以使用以下方法构造的二进制搜索树的总数n个值。下图显示了一个可能的二进制搜索树,其键值为3。因此,我们总共可以构建五棵二进制搜索树。当我们选择节点1作为根节点时,我们得到两棵树。类似地,一棵树以2为根节点,而当我们选择3作为根节点时为两棵树。
此方法涉及递归选择一个节点作为根节点并创建可能的二叉搜索树。
一种简单的计算可能的二叉搜索树总数的方法是通过加泰罗尼亚语数字:
算法
定义Node类,它具有三个属性,即: 左和右数据。在这里,左代表节点的左子节点,右代表节点的右子节点。
创建节点时,数据将传递到该节点的data属性,并且左右都将设置为null。
定义另一个具有属性根的类。 Root 表示树的根节点,并将其初始化为null。
a。 numOfBST()将找出给定密钥的总可能的二进制搜索树:
它将通过调用factorial()来计算给定密钥的加泰罗尼亚语数字。
加泰罗尼亚数字可以使用以下公式计算:
Cn =(2n)!/n! *(n + 1)!
Factorial()将计算给定数字的阶乘。
程序:
public class BinarySearchTree {
//Represent the node of binary tree
public static class Node{
int data;
Node left;
Node right;
public Node(int data){
//Assign data to the new node, set left and right children to null
this.data = data;
this.left = null;
this.right = null;
}
}
//Represent the root of binary tree
public Node root;
public BinarySearchTree(){
root = null;
}
//factorial() will calculate the factorial of given number
public int factorial(int num) {
int fact = 1;
if(num == 0)
return 1;
else {
while(num > 1) {
fact = fact * num;
num--;
}
return fact;
}
}
//numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key
public int numOfBST(int key) {
int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));
return catalanNumber;
}
public static void main(String[] args) {
BinarySearchTree bt = new BinarySearchTree();
//Display total number of possible binary search tree with key 5
System.out.println("Total number of possible Binary Search Trees with given key: " + bt.numOfBST(5));
}
}
输出:
Total number of possible Binary Search Trees with given key: 42

