Java使用链接列表实现二叉树
在此程序中,我们需要通过插入节点并按顺序显示节点来创建二叉树。典型的二叉树可以表示如下:
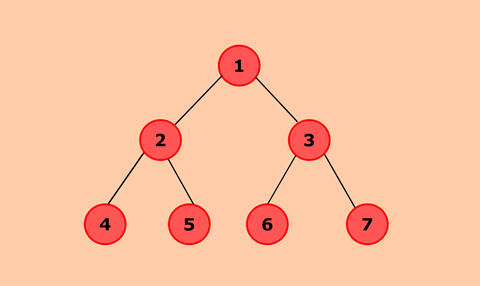
在二叉树中,每个节点最多可以有两个字节点。每个节点可以有零个,一个或两个字节点。二进制树中的每个节点都包含以下信息:

数据,它表示存储在节点中的值。
左 >表示指向左孩子的指针。
右表示指向右孩子的指针。
算法
定义Node类,它具有三个属性,即: 左和右数据。在这里,左代表节点的左子节点,右代表节点的右子节点。
创建节点后,数据将传递到该节点的data属性,并且左右都将设置为null。
定义另一个具有属性根的类。 Root代表树的根节点,并将其初始化为null。
a.insert()将向树中添加一个新节点:
它检查根是否为空,这意味着树为空。它将新节点添加为root。
否则,它将把root添加到队列中。
变量节点代表当前节点。
首先,它检查节点是否具有左右子节点。如果是,它将两个节点都添加到队列中。
如果不存在左子节点,则会将新节点添加为左子节点。
如果存在左侧,则它将新节点添加为右侧子节点。
a.Inorder()将以有序的方式显示树的节点。
它遍历整棵树,然后打印出左孩子,然后打印根,然后打印右孩子。
程序:
public class BinarySearchTree {
//Represent the node of binary tree
public static class Node{
int data;
Node left;
Node right;
public Node(int data){
//Assign data to the new node, set left and right children to null
this.data = data;
this.left = null;
this.right = null;
}
}
//Represent the root of binary tree
public Node root;
public BinarySearchTree(){
root = null;
}
//factorial() will calculate the factorial of given number
public int factorial(int num) {
int fact = 1;
if(num == 0)
return 1;
else {
while(num > 1) {
fact = fact * num;
num--;
}
return fact;
}
}
//numOfBST() will calculate the total number of possible BST by calculating Catalan Number for given key
public int numOfBST(int key) {
int catalanNumber = factorial(2 * key)/(factorial(key + 1) * factorial(key));
return catalanNumber;
}
public static void main(String[] args) {
BinarySearchTree bt = new BinarySearchTree();
//Display total number of possible binary search tree with key 5
System.out.println("Total number of possible Binary Search Trees with given key: " + bt.numOfBST(5));
}
}
输出:
Binary tree after insertion
1
Binary tree after insertion
2 1 3
Binary tree after insertion
4 2 5 1 3
Binary tree after insertion
4 2 5 1 6 3 7


