AI 命题逻辑
命题逻辑(PL)是最简单的逻辑形式,其中所有陈述都是由命题构成的。命题是一个陈述性陈述,它是对还是错。这是一种逻辑和数学形式的知识表示技术。
示例:
a) It is Sunday.
b) The Sun rises from West (False proposition)
c) 3+3= 7(False proposition)
d) 5 is a prime number.
以下是有关命题逻辑的一些基本事实:
命题逻辑也称为布尔逻辑,因为它适用于0和1、
在命题逻辑中,我们使用符号变量来表示逻辑,并且可以使用任何符号来表示命题,例如A,B,C,P,Q,R等。
命题可以是对,也可以是假,但不能两者都做。
命题逻辑由一个对象,关系或函数以及逻辑连接词组成。
这些连接词也称为逻辑运算符。
命题和连接词是命题逻辑的基本要素。
连接词可以说是连接两个句子的逻辑运算符。
一个始终为真的命题公式称为重言式,也称为有效句子。
始终为假的命题公式称为矛盾。
具有真值和假值的命题公式称为
问题,命令或意见之类的陈述不是命题,例如" Rohini在哪里"," 你好"," 你是什么人"名称",不是命题。
命题逻辑的语法:
命题逻辑的语法定义了知识表示形式所允许的句子。命题有两种类型:
原子命题
复合命题
原子命题: 原子命题是简单的命题。它由单个命题符号组成。这些句子必须为真或为假。
示例:
a) 2+2 is 4, it is an atomic proposition as it is a true fact.
b) "The Sun is cold" is also a proposition as it is a false fact.
复合命题: 复合命题是通过使用括号和逻辑连接词将简单或原子命题组合而成的。
示例:
a) "It is raining today, and street is wet."
b) "Ankit is a doctor, and his clinic is in Mumbai."
逻辑连接词:
逻辑连接词用于连接两个更简单的命题或逻辑上表示一个句子。我们可以借助逻辑连接词来创建复合命题。主要有五个连接词,如下所示:
否定词: 诸如¬P的句子称为P的否定词。文字可以是正文字或负文字。
连词: 具有∧连词(例如 P∧Q )的句子称为连词。
示例: Rohan聪明而勤奋。可以这样写:
P =罗汉很聪明,
Q =罗汉很努力。 →P∧Q 。
析取语: 具有∨连词的句子,例如 P∨Q 。称为析取,其中P和Q是命题。
示例: " Ritika是医生或工程师" ,
这里P = Ritika是Doctor。 Q = Ritika是Doctor,所以我们可以将其写为 P∨Q 。
蕴涵: 诸如P→Q之类的句子称为蕴涵。隐含也称为if-then规则。可以表示为
如果正在下雨,则街道是湿的。
令P =正在下雨,Q =街道是湿的,因此表示为P→问
双条件语句: 诸如P⇔Q这样的句子是双条件语句,例如如果我呼吸,那么我还活着
P =我在呼吸, Q =我还活着,可以表示为P⇔Q。
以下是命题逻辑连接词的摘要表:
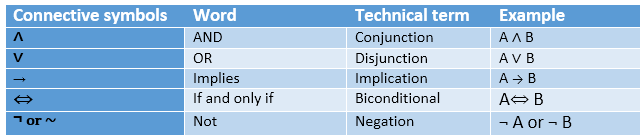
真值表:
在命题逻辑中,我们需要知道所有可能情况下命题的真值。我们可以将所有可能的组合与逻辑连接词组合在一起,这些组合以表格格式的表示称为
真值表。以下是所有逻辑连接词的真值表:
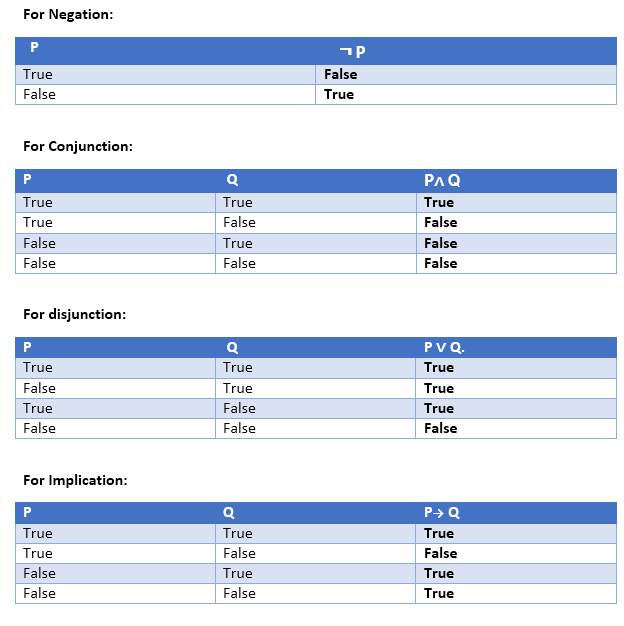
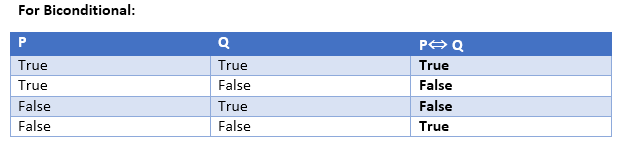
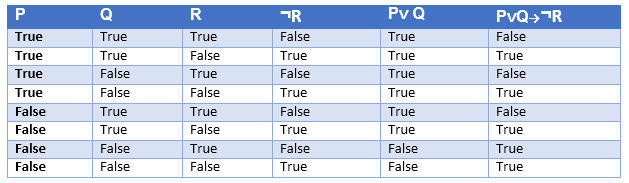
包含三个命题的真值表:
我们可以建立一个由三个命题P,Q和R组成的命题。这个真值表由8n个元组组成,因为我们采用了三个命题符号。
连接词的优先级:
就像算术运算符一样,命题连接器也有一个优先顺序或逻辑运算符。在评估命题问题时,应遵循此顺序。以下是运算符的优先顺序列表:
| 优先级 |
操作员 |
| 第一优先 |
肢体瘫痪 |
| 第二优先 |
否定 |
| 第三优先 |
连词(AND) |
| 第四优先 |
Disjunction(OR) |
| 第五优先 |
含义 |
| 六个优先级 |
双条件 |
注意: 为更好地理解,请使用括号确保正确的解释。例如∨RQ,可以解释为(¬R)Q。
逻辑对等:
逻辑对等是命题逻辑的特征之一。当且仅当真值表中的列彼此相同时,两个命题才在逻辑上相等。
让我们采用两个命题A和B,因此对于逻辑上的等价关系,我们可以将其写为A ⇔B。在下面的真值表中,我们可以看到¬A∨B和A→B的列相同,因此A等效于B

运算符的属性:
通透性: P∧Q = Q∧P,或 P∨Q = Q∨P。
关联性: (P∧Q)∧R = P∧(Q∧R), (P∨Q)∨R = P∨(Q∨R)
身份元素: P∧True = P, P∨True = True。
发行版: P 1(Q R)=(P Q)(P R)。
P∨(Q∧R)=(P∨Q)∧(P∨R)。
DE摩根定律: ¬(P∧Q)=(¬P)∨(¬Q) ¬(P∨Q)=(¬P)∧(¬Q)。
双重否定消除: ¬(¬P)= P。
命题逻辑的局限性:
我们不能用命题逻辑来表示所有,某些或全无的关系。例: 所有女孩都很聪明。 有些苹果很甜。
命题逻辑的表达能力有限。
在命题逻辑中,我们不能根据语句的属性或逻辑关系来描述语句。





