AVL 树

如果二叉搜索树的输入以排序（升序或降序）方式出现怎么办？然后它看起来像这样-

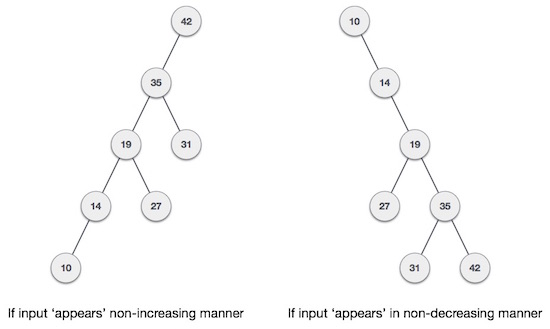
观察到BST的最坏情况性能最接近线性搜索算法，即Ο(n)。在实时数据中，我们无法预测数据模式及其频率。因此，需要平衡现有的 BST。

以他们的发明者 Adelson、 Velski 和 Landis 命名， AVL 树 是高度平衡的二叉搜索树。 AVL 树检查左右子树的高度，并确保差异不大于 1、这种差异称为 Balance Factor。

这里我们看到第一棵树是平衡的，接下来的两棵树是不平衡的-

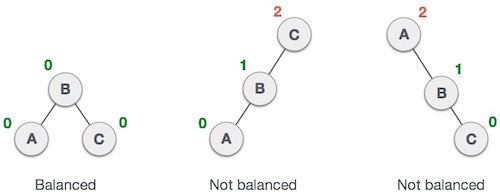
在第二棵树中， C的左子树高度为2，右子树高度为0，所以差为2、在第三棵树中， A的右子树 高度为 2，左边缺失，所以为 0，差值又为 2、 AVL 树允许差异（平衡因子）仅为 1、

BalanceFactor = height(left-sutree) − height(right-sutree)

如果左右子树的高度差大于1，则使用一些旋转技术来平衡树。

AVL 轮换

为了平衡自身，AVL 树可能会执行以下四种旋转-

左旋转右旋转左右旋转左右旋转

前两轮为单轮，后两轮为双轮。要有不平衡的树，我们至少需要一棵高度为 2 的树。有了这个简单的树，我们来一一理解。

如果一棵树变得不平衡，当一个节点被插入到右子树的右子树中时，我们执行一次左旋转-

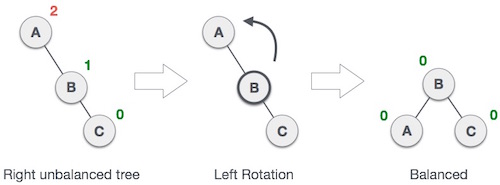
在我们的示例中，节点 A 变得不平衡，因为节点被插入到 A 的右子树的右子树中。我们通过使 A 成为 B 的左子树来执行左旋转。

如果在左子树的左子树中插入一个节点，AVL 树可能会变得不平衡。然后树需要正确旋转。

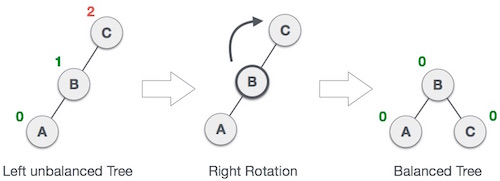
如图所示，不平衡节点通过执行右旋转成为其左孩子的右孩子。

双重旋转是已经解释过的旋转版本的稍微复杂的版本。为了更好地理解它们，我们应该注意旋转时执行的每个动作。让我们首先检查如何执行左右旋转。左右旋转是左旋转后右旋转的组合。

状态	动作
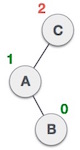	一个节点已经插入到左子树的右子树中。这使得 C 成为一个不平衡的节点。这些场景会导致 AVL 树执行左右旋转。
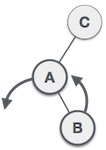	我们首先对C的左子树进行左旋转。这使得 A 成为 B 的左子树。
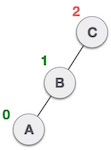	节点C仍然不平衡，但是现在，是因为左子树的左子树。
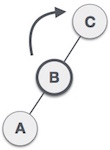	我们现在将树右旋，使 B 成为这个子树的新根节点。 C 现在成为它自己的左子树的右子树。
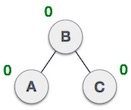	树现在平衡了。

第二种双重旋转是左右旋转。它是右旋后左旋的组合。

状态	动作
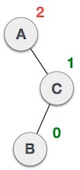	一个节点已经插入到右子树的左子树中。这使得 A 成为平衡因子为 2 的不平衡节点。
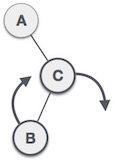	首先，我们沿C节点进行右旋转，使C成为自己左子树的右子树乙。现在，B 成为 A 的右子树。
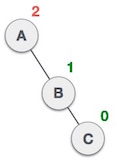	节点A由于其右子树的右子树仍然不平衡，需要向左旋转。
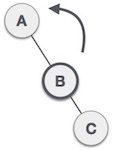	通过使B成为子树的新根节点来执行左旋转。 A 成为其右子树 B 的左子树。
	树现在平衡了。

找工作要求35岁以下，35岁以上的程序员都干什么去了？

长久以来，一直有一个问题困扰着技术人——如何打破“程序员的35岁职业魔咒”，这一天迟早会到来，或早或晚。

昵称：邮箱：