搜索

Linear Search ( Array A, Value x)
Step 1: Set i to 1
Step 2: if i > n then go to step 7
Step 3: if A[i] = x then go to step 6
Step 4: Set i to i + 1
Step 5: Go to Step 2
Step 6: Print Element x Found at index i and go to step 8
Step 7: Print element not found
Step 8: Exit

procedure linear_search (list, value)
   for each item in the list
      if match item == value
         return the item's location
      end if
   end for
end procedure

mid = low + (high-low) / 2

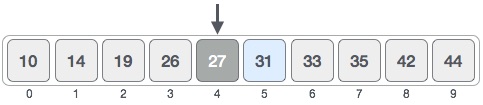
low = mid + 1
mid = low + (high-low) / 2

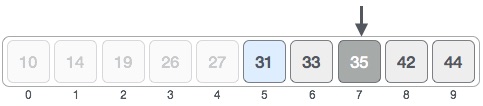
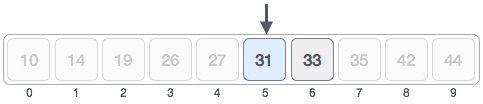
Procedure binary_search
   A ← sorted array
   n ← size of array
   x ← value to be searched
   Set lowerBound = 1
   Set upperBound = n 
   while x not found
      if upperBound < lowerBound 
         EXIT: x does not exists.
   
      set midPoint = lowerBound + ( upperBound-lowerBound ) / 2
      
      if A[midPoint] < x
         set lowerBound = midPoint + 1
         
      if A[midPoint] > x
         set upperBound = midPoint -1 
      if A[midPoint] = x 
         EXIT: x found at location midPoint
   end while
   
end procedure

mid = Lo + ((Hi-Lo) / (A[Hi]-A[Lo])) * (X-A[Lo])
where −
   A    = list
   Lo   = Lowest index of the list
   Hi   = Highest index of the list
   A[n] = Value stored at index n in the list

Step 1 − Start searching data from middle of the list.
Step 2 − if it is a match, return the index of the item, and exit.
Step 3 − if it is not a match, probe position.
Step 4 − Divide the list using probing formula and find the new midle.
Step 5 − if data is greater than middle, search in higher sub-list.
Step 6 − if data is smaller than middle, search in lower sub-list.
Step 7 − Repeat until match.

A → Array list
N → Size of A
X → Target Value
Procedure Interpolation_Search()
   Set Lo  →  0
   Set Mid →-1
   Set Hi  →  N-1
   while X does not match
   
      if Lo equals to Hi OR A[Lo] equals to A[Hi]
         EXIT: Failure, Target not found
      end if
      
      Set Mid = Lo + ((Hi-Lo) / (A[Hi]-A[Lo])) * (X-A[Lo]) 
      if A[Mid] = X
         EXIT: Success, Target found at Mid
      else 
         if A[Mid] < X
            Set Lo to Mid+1
         else if A[Mid] > X
            Set Hi to Mid-1
         end if
      end if
   End While
End Procedure