快速排序
快速排序是一种高效的排序算法,它基于将数据数组划分为更小的数组。一个大数组被划分为两个数组,其中一个数组保存的值小于指定值(例如枢轴),根据该值进行分区,另一个数组保存大于枢轴值的值。
Quicksort 对数组进行分区,然后递归调用自身两次以对两个结果子数组进行排序。该算法对于大型数据集非常有效,因为它的平均复杂度和最坏情况复杂度分别为 O(n
2)。
快速排序中的分区
以下动画演示说明了如何在数组中找到枢轴值。
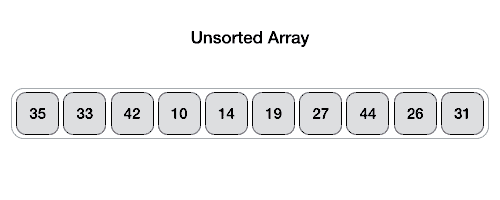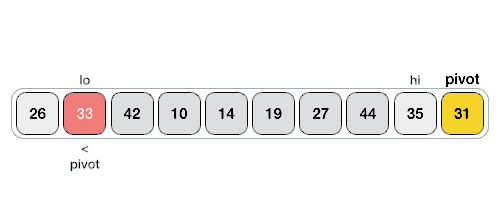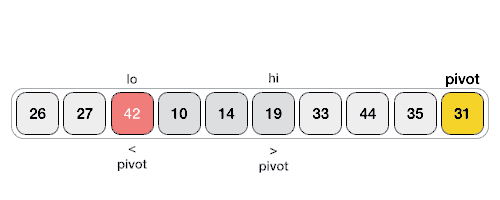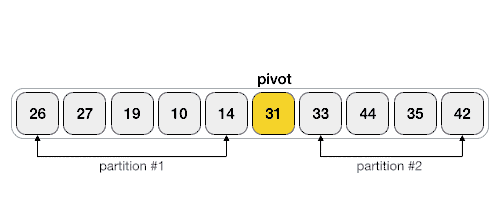
枢轴值将列表分为两部分。并且递归地,我们找到每个子列表的枢轴,直到所有列表只包含一个元素。
快速排序枢轴算法
基于我们对快速排序中分区的理解,我们现在尝试为它编写一个算法,如下所示。
Step 1 − Choose the highest index value has pivot
Step 2 − Take two variables to point left and right of the list excluding pivot
Step 3 − left points to the low index
Step 4 − right points to the high
Step 5 − while value at left is less than pivot move right
Step 6 − while value at right is greater than pivot move left
Step 7 − if both step 5 and step 6 does not match swap left and right
Step 8 − if left ≥ right, the point where they met is new pivot
快速排序枢轴伪代码
上述算法的伪代码可以推导出为-
function partitionFunc(left, right, pivot)
leftPointer = left
rightPointer = right-1
while true do
while A[++leftPointer] < pivot do
//do-nothing
end while
while rightPointer > 0 && A[--rightPointer] > pivot do
//do-nothing
end while
if leftPointer >= rightPointer
break
else
swap leftPointer,rightPointer
end if
end while
swap leftPointer,right
return leftPointer
end function
快速排序算法
递归地使用枢轴算法,我们最终得到更小的可能分区。然后处理每个分区以进行快速排序。我们为快速排序定义递归算法如下-
Step 1 − Make the right-most index value pivot
Step 2 − partition the array using pivot value
Step 3 − quicksort left partition recursively
Step 4 − quicksort right partition recursively
快速排序伪代码
要深入了解它,让我们看看快速排序算法的伪代码-
procedure quickSort(left, right)
if right-left <= 0
return
else
pivot = A[right]
partition = partitionFunc(left, right, pivot)
quickSort(left,partition-1)
quickSort(partition+1,right)
end if
end procedure

