递归基础
一些计算机编程语言允许模块或函数调用自身。这种技术称为递归。在递归中,函数
α 要么直接调用自身,要么调用函数
β,该函数又调用原始函数
α。
α函数称为递归函数。
示例-一个调用自身的函数。
int function(int value) {
if(value < 1)
return;
function(value-1);
printf("%d ",value);
}
示例-一个函数调用另一个函数,该函数又再次调用它。
int function1(int value1) {
if(value1 < 1)
return;
function2(value1-1);
printf("%d ",value1);
}
int function2(int value2) {
function1(value2);
}
属性
递归函数可以像循环一样无限循环。为避免递归函数无限运行,递归函数必须具备两个属性-
基本条件-必须至少有一个基本条件或条件,这样,当满足此条件时,函数将停止递归调用自身。
渐进式方法-递归调用应该以这样一种方式进行,即每次进行递归调用时,它都更接近基本标准。
实施
许多编程语言通过
堆栈实现递归。通常,每当一个函数(
caller)调用另一个函数(
callee)或自身作为被调用者时,调用者函数将执行控制权转移给被调用者。这个传输过程还可能涉及一些数据从调用者传递给被调用者。
这意味着,调用函数必须暂时暂停其执行,并在执行控制从被调用函数返回时恢复。在这里,调用者函数需要准确地从它自己暂停的执行点开始。它还需要与它正在处理的完全相同的数据值。为此,会为调用者函数创建一个激活记录(或堆栈帧)。
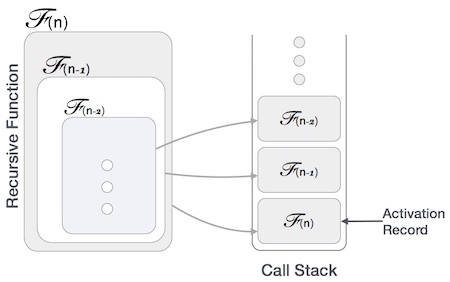
此激活记录保存有关局部变量、形参、返回地址和所有传递给调用函数的信息。
递归分析
人们可能会争论为什么要使用递归,因为同样的任务可以通过迭代来完成。第一个原因是,递归使程序更具可读性,并且由于最新增强的 CPU 系统,递归比迭代更有效。
时间复杂度
在迭代的情况下,我们采用迭代次数来计算时间复杂度。同样,在递归的情况下,假设一切都是不变的,我们试图找出递归调用的次数。对函数的调用是 Ο(1),因此递归调用的 (n) 次使得递归函数为 Ο(n)。
空间复杂度
空间复杂度被计算为模块执行所需的额外空间量。在迭代的情况下,编译器几乎不需要任何额外的空间。编译器不断更新迭代中使用的变量的值。但是在递归的情况下,每次进行递归调用时,系统都需要存储激活记录。因此,认为递归函数的空间复杂度可能会高于迭代函数的空间复杂度。



