Statistics Beta 分布
β 分布表示由两个正形状参数 $ \alpha $ 和 $ \beta $ 参数化的连续概率分布,它们作为随机变量 x 的指数出现并控制分布的形状。
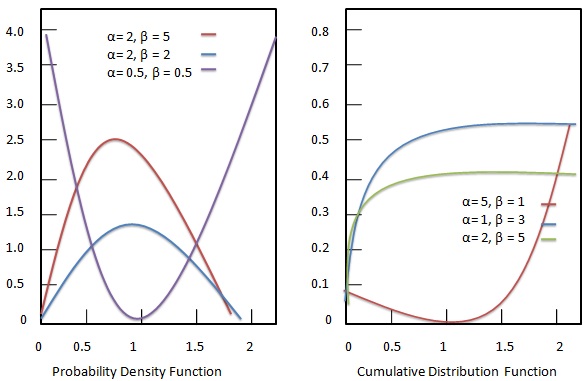
概率密度函数
Beta 分布的概率密度函数为:
公式
${ f(x) = \frac{(xa)^{\alpha-1}(bx)^{\beta-1}}{B(\alpha,\beta) (ba)^{\alpha+\beta-1}} \hspace{.3in} a \le x \le b; \alpha, \beta > 0 \\[7pt] \, 其中 \ B(\alpha,\beta) = \int_{0}^{1} {t^{\alpha-1}(1-t)^{ \beta-1}dt} }$
哪里-
${ \alpha, \beta }$ = 形状参数。
${a, b}$ = 上限和下限。
${B(\alpha,\beta)}$ = Beta 函数。
标准 Beta 版分发
在上下界为 1 和 0 的情况下,beta 分布称为标准 beta 分布。它由以下公式驱动:
公式
${ f(x) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)} \hspace{.3in} \le x \le 1; \alpha, \beta > 0}$
累积分布函数
Beta 分布的累积分布函数为:
公式
${ F(x) = I_{x}(\alpha,\beta) = \frac{\int_{0}^{x}{t^{\alpha-1}(1-t)^{\beta-1}dt}}{B(\alpha,\beta)} \hspace{.2in} 0 \le x \le 1; p, \beta > 0 }$
哪里-
${ \alpha, \beta }$ = 形状参数。
${a, b}$ = 上限和下限。
${B(\alpha,\beta)}$ = Beta 函数。
也称为不完全贝塔函数比。



