Statistics 中心极限定理
如果抽取样本的总体是正态总体,则
样本均值将等于总体均值,
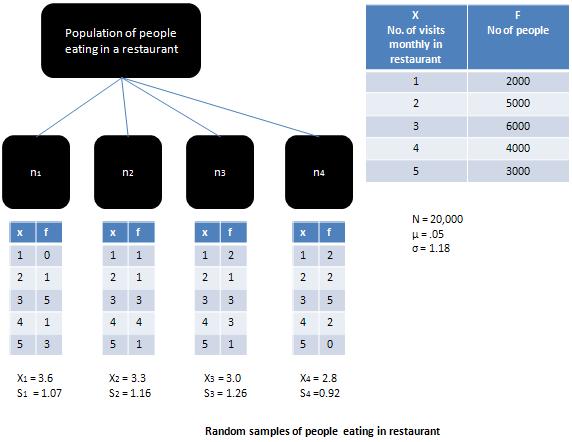
抽样分布将是正态分布。当更多的总体偏斜时(如图所示的情况),如果样本很大(即大于 30),
抽样分布将趋向于接近正态分布。
根据
中心极限定理,对于大小大于30的足够大的样本,
采样分布的形状会越来越像
正态分布分布,与父种群的形状无关。这个定理解释了
人口分布和
抽样分布之间的关系。它强调了一个事实,如果有足够大的样本集,则
采样分布的均值接近
正态分布。 Richard 总结了中心极限定理的重要性。一、莱文用以下的话来说:
中心极限定理的意义在于,它允许我们使用样本统计量来推断总体参数,而无需了解总体频率分布的形状,除了我们可以从样本中获得的信息。