Statistics 峰度
分布的拖尾程度由峰度测量。它告诉我们分布在多大程度上比正态分布更容易出现异常值(更重或轻尾)。由 Investopedia 提供的三种不同类型的曲线如下所示-
很难从密度图(左图)中辨别出不同类型的峰度,因为所有分布的尾部都接近于零。但是在正常的分位数-分位数图中很容易看到尾部的差异(右图)。
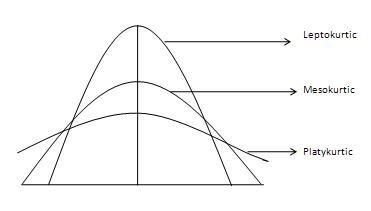
正态曲线称为 Mesokurtic 曲线。如果分布曲线比正态曲线或中峰曲线更容易出现异常(或尾部更重),则它被称为 Leptokurtic 曲线。如果一条曲线比正常曲线更不容易出现异常(或尾部较浅),则称为 platykurtic 曲线。峰度由矩测量,由以下公式给出-
公式
${\beta_2 = \frac{\mu_4}{\mu_2}}$
哪里-
${\mu_4 = \frac{\sum(x-\bar x)^4}{N}}$
\beta_2 的值越大,曲线越尖峰或越尖峰。正常曲线的值为 3,leptokurtic 的 \beta_2 大于 3,而 platykurtic 的 \beta_2 小于 3、
示例
问题说明:
给出了一家工厂 45 名工人的日工资数据。使用关于均值的矩计算 \beta_1 和 \beta_2、对结果发表评论。
| 工资(卢比) |
工人数量 |
| 100-200 |
1 |
| 120-200 |
2 |
| 140-200 |
6 |
| 160-200 |
20 |
| 180-200 |
11 |
| 200-200 |
3 |
| 220-200 |
2 |
解决方案:
| 工资(卢比) |
工人数量(f) |
中点米 |
m-${\frac{170}{20}}$ d |
${fd}$ |
${fd^2}$ |
${fd^3}$ |
${fd^4}$ |
| 100-200 |
1 |
110 |
-3 |
-3 |
9 |
-27 |
81 |
| 120-200 |
2 |
130 |
-2 |
-4 |
8 |
-16 |
32 |
| 140-200 |
6 |
150 |
-1 |
-6 |
6 |
-6 |
6 |
| 160-200 |
20 |
170 |
0 |
0 |
0 |
0 |
0 |
| 180-200 |
11 |
190 |
1 |
11 |
11 |
11 |
11 |
| 200-200 |
3 |
210 |
2 |
6 |
12 |
24 |
48 |
| 220-200 |
2 |
230 |
3 |
6 |
18 |
54 |
162 |
| |
${N=45}$ |
|
|
${\sum fd = 10}$ |
${\sum fd^2 = 64}$ |
${\sum fd^3 = 40}$ |
${\sum fd^4 = 330}$ |
由于偏差是从假设的平均值中获取的,因此我们首先计算关于任意原点的矩,然后计算关于平均值的矩。关于任意原点'170'的时刻
${\mu_1^1= \frac{\sum fd}{N} \times i = \frac{10}{45} \times 20 = 4.44 \\[7pt] \mu_2^1= \frac{\sum fd ^2}{N} \times i^2 = \frac{64}{45} \times 20^2 =568.88 \\[7pt] \mu_3^1= \frac{\sum fd^2}{N} \次 i^3 = \frac{40}{45} \times 20^3 =7111.11 \\[7pt] \mu_4^1= \frac{\sum fd^4}{N} \times i^4 = \frac {330}{45} \times 20^4 =1173333.33 }$
关于平均的时刻
${\mu_2 = \mu'_2-(\mu'_1 )^2 = 568.88-(4.44)^2 = 549.16 \\[7pt] \mu_3 = \mu'_3-3(\mu'_1)(\ mu'_2) + 2(\mu'_1)^3 \\[7pt] \, = 7111.11-(4.44) (568.88)+ 2(4.44)^3 \\[7pt] \, = 7111.11-7577.48+175.05 =-291.32 \\[7pt] \\[7pt] \mu_4= \mu'_4-4(\mu'_1)(\mu'_3) + 6 (\mu_1 )^2 (\mu'_2)-3 (\mu'_1)^4 \\[7pt] \, = 1173333.33-4 (4.44)(7111.11)+6(4.44)^2 (568.88)-3(4.44)^4 \\[7pt] \, = 1173333.33-126293.31+67288.03-1165.87 \\[7pt] \, = 1113162.18 }$
从关于均值的运动值,我们现在可以计算 ${\beta_1}$ 和 ${\beta_2}$:
${\beta_1 = \mu^2_3 = \frac{(-291.32)^2}{(549.16)^3} = 0.00051 \\[7pt] \beta_2 = \frac{\mu_4}{(\mu_2)^2 } = \frac{1113162.18}{(546.16)^2} = 3.69 }$
从上面的计算可以得出结论,衡量偏度的${\beta_1}$几乎为零,从而表明分布几乎是对称的。 ${\beta_2}$ 测量峰度,其值大于 3,因此暗示分布是细峰态。

