Statistics 正态分布
正态分布是数据集的一种排列,其中大多数值聚集在范围的中间,其余的值对称地向任一极端递减。身高是遵循正态分布模式的一个简单例子:大多数人的身高是平均的,比平均身高高和矮的人数相当相等,而极少数(仍然大致相当)的人数要么是极端的高或极矮。以下是正态分布曲线示例:
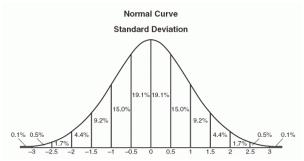
正态分布的图形表示有时被称为钟形曲线,因为它呈喇叭形。精确的形状可以根据人口的分布而变化,但峰值总是在中间,曲线总是对称的。在正态分布中,均值众数和中位数都相同。
公式
${y = \frac{1}{\sqrt {2 \pi}}e^{\frac{-(x-\mu)^2}{2 \sigma}} }$
哪里-
${\mu}$ = 平均值
${\sigma}$ = 标准差
${\pi \approx 3.14159}$
${e \approx 2.71828}$
示例
问题说明:
一项每日旅行时间的调查得出以下结果(以分钟为单位):
| 26 |
33 |
65 |
28 |
34 |
55 |
25 |
44 |
50 |
36 |
26 |
37 |
43 |
62 |
35 |
38 |
45 |
32 |
28 |
34 |
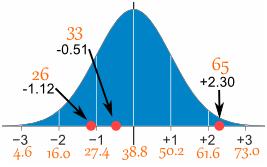
平均值为 38.8 分钟,标准差为 11.4 分钟。将值转换为 z-分数并准备正态分布图。
解决方案:
我们一直使用的 z-score 公式:
${z = \frac{x-\mu}{\sigma} }$
哪里-
${z}$ = "z 分数"(标准分数)
${x}$ = 要标准化的值
${\mu}$ = 平均值
${\sigma}$ = 标准差
要转换为 26:
先减去均值:26-38.8 =-12.8,
然后除以标准差:-12.8/11.4 =-1.12
所以 26 是-1.12 与平均值的标准差
这是前三个转换。
| 原始值 |
计算 |
标准分数(z-score) |
| 26 |
(26-38.8)/11.4 = |
-1.12 |
| 33 |
(33-38.8)/11.4 = |
-0.51 |
| 65 |
(65-38.8)/11.4 = |
-2.30 |
| ... |
... |
... |
这里用图形表示: