Statistics 维恩图
维恩图是一种直观表示实体或对象组之间关系的方法。维恩图由圆圈组成,其中每个圆圈代表一整套。维恩图可以有无限的圆,但通常最好有两个或三个圆,否则图会变得太复杂。
绘制维恩图的步骤
考虑以下人群:
板球运动员-$ C = \{ Ram、Shyam、Mohan、Rohan、Ramesh、Suresh \} $
曲棍球运动员-$ H = \{ Ramesh、Naresh、Mahesh、Leela、Sunita \} $
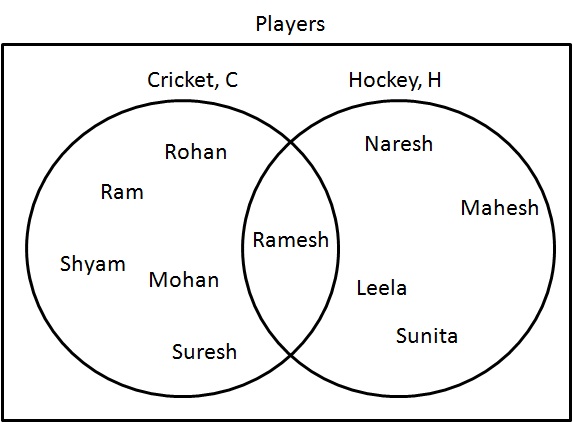
第 1 步:绘制一个矩形并将其标记为玩家。
第 2 步:绘制两个圆圈并将它们标记为板球和曲棍球。确保圆圈相互重叠。
第 3 步:在圆圈内写下相关的名称。通用名称应属于共同区域。
联合
Union ($ \cup $) 表示一个集合,其中项目存在于所有类别中但不重复。
示例
问题说明:
绘制$ C \cup H $的维恩图。
解决方案:
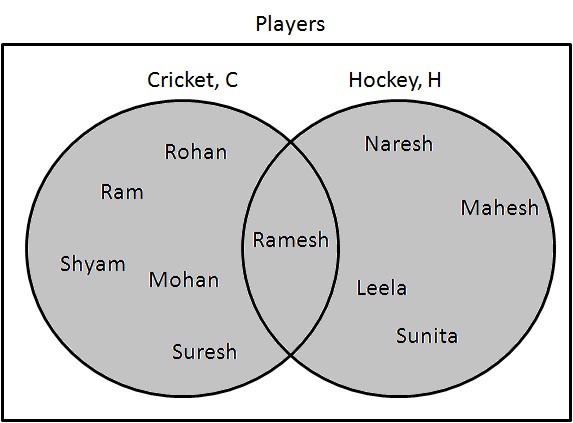
第 1 步:确定正在打板球或曲棍球的球员。绘制它们如下:
$ C \cup H = \{ Ram, Shyam, Mohan, Rohan, Ramesh, Suresh, Naresh, Mahesh, Leela, Sunita \} $.
交叉路口
交集 ($ \cap $) 表示两个类别中都存在项目的集合。
示例
问题说明:
绘制$ C \cap H $的维恩图。
解决方案:
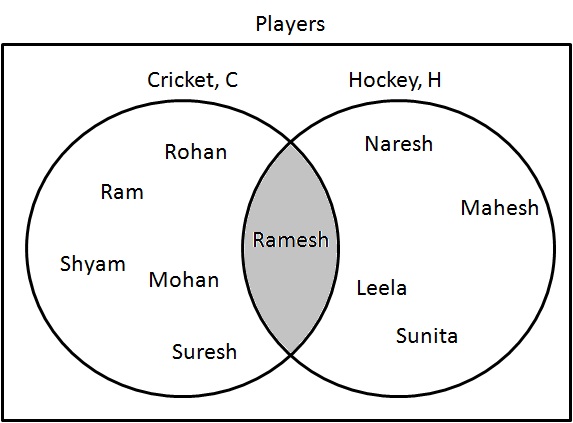
第 1 步:确定同时打板球和曲棍球的球员。绘制它们如下:
$ C \cap H = \{ Ramesh \} $.
区别
Difference ($-$) 表示一个集合,其中项目仅出现在一个类别中,而不出现在其他类别中。
示例
问题说明:
绘制 $ C-H $ 的维恩图。
解决方案:
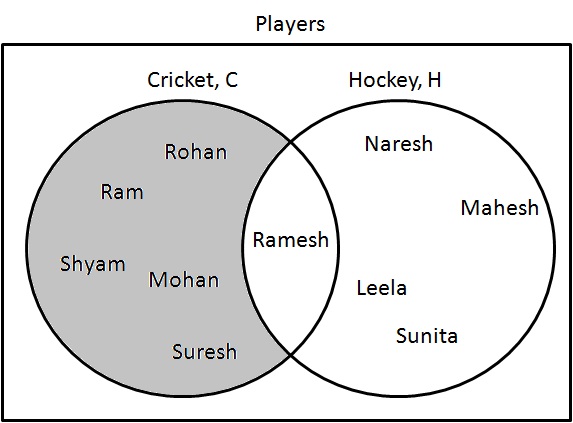
第 1 步:确定只打板球的球员。绘制它们如下:
$ C-H = \{ Ram、Shyam、Mohan、Rohan、Suresh \} $.